Back to LING 385
Lecture 13
SGD for the simplest NN
- let zd = desired output, zc = computed output by NN.
- assume we have lots of training data of pairs (x, zd) for learning
- computed output zc = wx + b
- a = Sigmoid(z)
- da/dz = a(1 − a)
- loss function L = 1/2(zc − zd)^2
- derivatives: dz/db = 1, dz/dx = w, dz/dw = x, dL/dzc = (zc − zd).
- remember chain rule a → b → c: dc/da = (db/da)(dc/db).
- learn w and b from data pairs (x1, zd1), (x2, zd2), (xi, zdi), (xk, zdk)...
- choose any random w and b and repeat
- pick pair (xi, zdi) to learn from.
- if updating bias, apply SGD formula for b: b(t) = b(t − 1) − η(zc − zdi).
- if updating weight, apply SGD formula for w
- the chain is w → zc → a → L
- therefore w(t) = w(t − 1) − ηxia(1 − a)(zc − zdi)
- repeat with pair (xk, zdk).
- after convergence, we now have the learned w and b
Greedy, Exhaustive, and Dynamic Programming
Greedy
- makes locally optimal choices at each stage with the hope of finding a global optimum
- chooses the best option at each step without considering the overall future consequences
- might not always lead to the globally optimal solution
- doesn't reconsider previous choices
- local optimum does not always result in global optimum
Exhaustive (Brute Force)
- considers all possible solutions and exhaustively evaluates each one
- guarantees finding the optimal solution by exploring the entire solution space.
- can be inefficient for large problem instances since it checks every possible path
Dynamic Programming
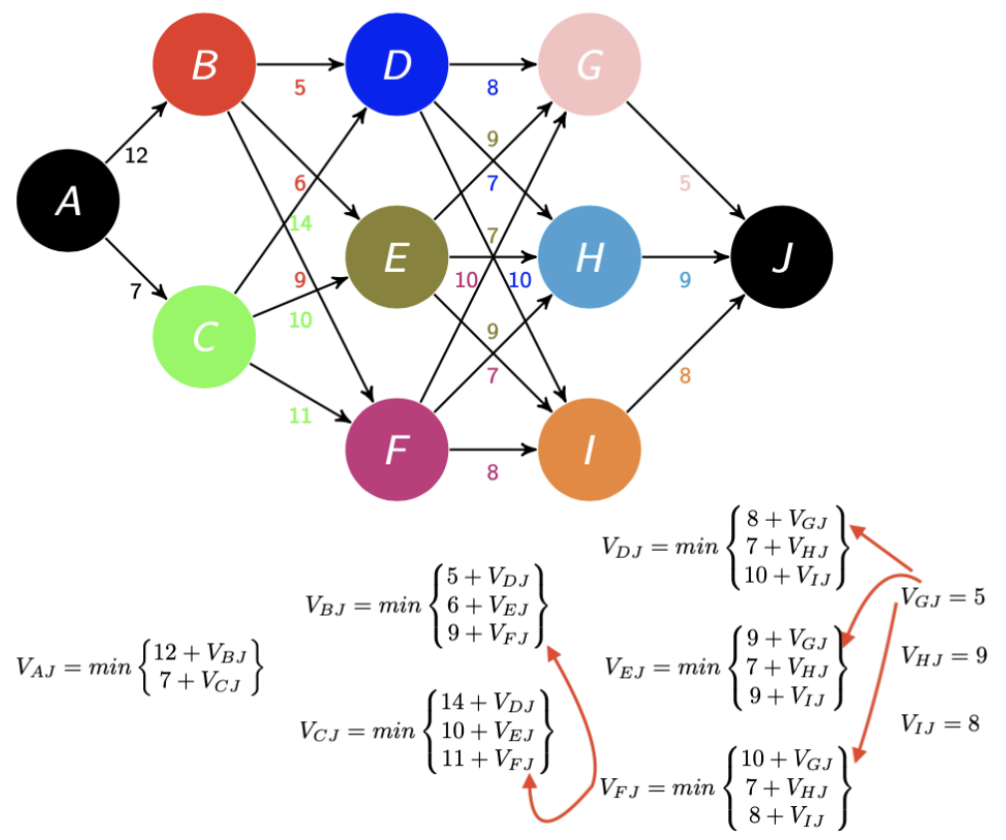
- breaks down a problem into smaller, overlapping subproblems
- solves each subproblem only once and stores the solutions
- avoids redundant computations
- can be implemented using a bottom-up approach (solving smaller subproblems first)
- more efficient than brute force approaches
- avoids redundant computations through this bottom-up approach
The Backpropagation Algorithm
- begin optimization at the last layer before the output
- focus on enhancing weights (w's) and biases (b's) at this layer
- utilize the refined information to update weights and biases in the preceding layer
- use dynamic programming to choose which neurons to update
- repeat the process iteratively, moving backward through the layers
- this technique is known as backpropagation
